压在透明的玻璃上c-国产精品国产一级A片精品免费-国产精品视频网-成人黄网站18秘 免费看|www.tcsft.com

2024年6月召開的中國科學(xué)院院士大會(huì)上，我應(yīng)邀作了一個(gè)以“數(shù)學(xué)與人工智能”為題的大會(huì)報(bào)告。會(huì)后許多院士都希望我把報(bào)告的主要內(nèi)容寫出來，這是這篇短文的由來。在這篇文章中，我試圖用相對(duì)通俗但又不掩蓋核心問題的語言解釋人工智能的一些主要方法和它們各自的特點(diǎn)。

人工智能的眾多不同方法，可以根據(jù)其所用數(shù)據(jù)量的大小，分為零數(shù)據(jù)、小數(shù)據(jù)、大數(shù)據(jù)和全數(shù)據(jù)方法。當(dāng)然，數(shù)據(jù)不是人工智能發(fā)展的唯一線索，但它可以比較方便地幫助我們梳理人工智能發(fā)展過程中出現(xiàn)的不同想法。

零數(shù)據(jù)

邏輯推理、符號(hào)計(jì)算、專家系統(tǒng)等原則上都不需要數(shù)據(jù)。邏輯推理方法的主要思路是構(gòu)造算法和軟件模仿人的推理過程。符號(hào)表示和符號(hào)計(jì)算試圖把邏輯推理更加形式化、自動(dòng)化。在1956年的達(dá)特茅斯(Dartmouth)會(huì)議上，紐厄爾(Newell)、肖(Shaw)和西蒙(Simon)推出的邏輯理論(Logic Theorist)系統(tǒng)就是一個(gè)這樣的例子。邏輯理論被認(rèn)為是第一個(gè)人工智能系統(tǒng)，它能夠證明許多數(shù)學(xué)定理，還能下棋。

專家系統(tǒng)的目標(biāo)是把專家知識(shí)用軟件系統(tǒng)實(shí)現(xiàn)運(yùn)用。專家系統(tǒng)最成功的例子是IBM的深藍(lán)(Deep Blue)，它在1997年戰(zhàn)勝了國際象棋冠軍卡斯帕羅夫(Kasparov)。其他零數(shù)據(jù)方法方面典型的工作包括LISP語言和數(shù)學(xué)定理機(jī)器證明的“吳方法”。

小數(shù)據(jù)

線性回歸、邏輯回歸、支持向量機(jī)等統(tǒng)計(jì)學(xué)習(xí)方法是典型的小數(shù)據(jù)方法。早期的神經(jīng)網(wǎng)絡(luò)，如感知機(jī)(perceptron)，也是小數(shù)據(jù)方法。隱式馬爾可夫過程(HMM)、N-gram、深度學(xué)習(xí)出現(xiàn)之前的機(jī)器學(xué)習(xí)方法等，也都是小數(shù)據(jù)方法。過去的模式識(shí)別、自然語言處理、語音技術(shù)、機(jī)器人技術(shù)等都是基于小數(shù)據(jù)（或零數(shù)據(jù)）方法實(shí)現(xiàn)的。很長(zhǎng)一段時(shí)間里，人工智能是靠這類方法支撐的。

零數(shù)據(jù)和小數(shù)據(jù)方法往往對(duì)簡(jiǎn)單問題（如跳棋、象棋等）比較有效，但是在復(fù)雜問題面前無能為力。具體地說，它難以克服“組合爆炸”和“維數(shù)災(zāi)難”引起的困難。組合爆炸是指當(dāng)系統(tǒng)變大的時(shí)候，所有可能出現(xiàn)的組合爆炸性增加。例如從國際象棋到圍棋（見圖1），棋盤從8×8變成19×19，其所有可能的組合增加了多個(gè)數(shù)量級(jí)。零數(shù)據(jù)方法雖然能夠解決國際象棋問題，卻難以解決圍棋問題。

圖1 國際象棋（左）與圍棋（右）棋盤（圖來自互聯(lián)網(wǎng)）

維數(shù)災(zāi)難是指當(dāng)一個(gè)問題的自由度（即維數(shù)）增加的時(shí)候，計(jì)算復(fù)雜性呈指數(shù)增加。小數(shù)據(jù)方法可以處理低維問題，但是難以處理高維問題。對(duì)于圖像識(shí)別、量子化學(xué)、動(dòng)態(tài)規(guī)劃和非線性統(tǒng)計(jì)等領(lǐng)域的高維問題，人們只能通過經(jīng)驗(yàn)、特征工程或者極端的簡(jiǎn)化方法處理。量子化學(xué)中的哈特里(Hartree)或者哈特里-福克(Hartree-Fock)方法，以及非線性統(tǒng)計(jì)中的廣義線性模型(generalized linear models)等都是極端簡(jiǎn)化方法的例子。

人工智能經(jīng)過了幾次大起大落，本質(zhì)上都是由于對(duì)組合爆炸和維數(shù)災(zāi)難的困難程度認(rèn)識(shí)不足引發(fā)的。最近幾年，我國仍有團(tuán)隊(duì)提出擺脫大數(shù)據(jù)、以小數(shù)據(jù)方法實(shí)現(xiàn)通用人工智能。這個(gè)方案的核心問題是它能否克服組合爆炸和維數(shù)災(zāi)難引起的困難。如果這種思路能夠有效解決圍棋問題，那么它和傳統(tǒng)的零數(shù)據(jù)、小數(shù)據(jù)方法必然有著本質(zhì)的不同。如果不能，那么基于這種思路建立的通用人工智能系統(tǒng)最多也只是一個(gè)“弱智”系統(tǒng)。這并不是說零數(shù)據(jù)、小數(shù)據(jù)方法在處理復(fù)雜問題時(shí)沒有用，而是說僅僅靠這些方法難以走得很遠(yuǎn)。我們必須對(duì)此有正確的認(rèn)識(shí)。

大數(shù)據(jù)

盡管深度學(xué)習(xí)受到熱捧之前人們就已經(jīng)在處理和分析大數(shù)據(jù)，但是真正讓大數(shù)據(jù)充分發(fā)揮作用的方法是深度學(xué)習(xí)，其標(biāo)志性事件是辛頓(Hinton)團(tuán)隊(duì)于2012年贏得ImageNet圖像識(shí)別比賽冠軍。辛頓等人設(shè)計(jì)并訓(xùn)練了一個(gè)神經(jīng)網(wǎng)絡(luò)，取名AlexNet。AlexNet有5層卷積網(wǎng)絡(luò)、3層全連接網(wǎng)絡(luò)，6000多萬個(gè)參數(shù)。相比較而言，之前楊立昆(Yann LeCun)訓(xùn)練的Le-Net只有幾萬個(gè)可訓(xùn)練參數(shù)。

需要強(qiáng)調(diào)的是，辛頓等人在訓(xùn)練AlexNet的時(shí)候用的主要算法，如隨機(jī)梯度下降、反向傳播等都是已知的。辛頓團(tuán)隊(duì)的工作就是充分訓(xùn)練了這樣一個(gè)多層神經(jīng)網(wǎng)絡(luò)。要做到這一點(diǎn)，就需要高質(zhì)量的數(shù)據(jù)資源和一定的算力資源。這正是ImageNet和GPU發(fā)揮作用的時(shí)候。所以辛頓等人的工作既是技術(shù)上的成功，更是信念上的堅(jiān)持帶來的成果。

辛頓等人的工作不僅改變了圖像識(shí)別，而且改變了整個(gè)人工智能領(lǐng)域，因?yàn)榛谏窠?jīng)網(wǎng)絡(luò)的深度學(xué)習(xí)方法是一個(gè)通用方法。神經(jīng)網(wǎng)絡(luò)其實(shí)就是一類函數(shù)，它與多項(xiàng)式這類函數(shù)的不同之處在于它似乎是逼近多變量函數(shù)的有效工具。也就是說，它能夠有效地幫助我們克服維數(shù)災(zāi)難和組合爆炸引起的困難。事實(shí)上，基于深度強(qiáng)化學(xué)習(xí)的人工智能方法，AlphaGo很快就在圍棋比賽中戰(zhàn)勝了人類最好的選手。神經(jīng)網(wǎng)絡(luò)也被用來解決科學(xué)領(lǐng)域碰到的多個(gè)自由度的問題，如蛋白結(jié)構(gòu)問題、分子動(dòng)力學(xué)勢(shì)能函數(shù)問題等，并由此催生出一個(gè)嶄新的科研范式：AI for Science。正因?yàn)樯疃葘W(xué)習(xí)在多變量函數(shù)逼近這樣一個(gè)非常基礎(chǔ)性的問題上帶來了巨大突破，所以它在各種各樣的問題上都給我們帶來了新的可能。

需要強(qiáng)調(diào)的是，盡管很多成功案例都表明深度學(xué)習(xí)方法是解決高維問題的一個(gè)有效工具，但我們對(duì)其背后的原因了解得還很不充分。從數(shù)學(xué)的角度來說，這是一個(gè)非常優(yōu)雅、非常清晰的數(shù)學(xué)問題，它將推動(dòng)高維分析的發(fā)展。關(guān)于這方面的工作，請(qǐng)參見我在2022年國際數(shù)學(xué)家大會(huì)上的報(bào)告。

早在20世紀(jì)40年代，麥卡洛克(McCulloch)和皮茨（Pitts）就提出了神經(jīng)網(wǎng)絡(luò)的概念。50年代，羅森布拉特（Rosenblatt）又提出了感知機(jī)的概念。為什么要一直等到2010年左右，人們才開始真正認(rèn)識(shí)到神經(jīng)網(wǎng)絡(luò)的巨大威力？我認(rèn)為其根本原因有兩個(gè)：一是訓(xùn)練好神經(jīng)網(wǎng)絡(luò)需要一定的高質(zhì)量數(shù)據(jù)和算力資源，這些條件是一個(gè)門檻；二是人們?nèi)狈?duì)神經(jīng)網(wǎng)絡(luò)的正確認(rèn)識(shí)。明斯基(Minsky)和佩珀特(Papert)合著了一本很著名的書，就叫“感知機(jī)”(Perceptron)。這本書研究的一個(gè)主要問題是：什么樣的邏輯函數(shù)可以用（兩層）感知機(jī)精確表示出來？結(jié)果他們發(fā)現(xiàn)，一些簡(jiǎn)單的邏輯函數(shù)都無法用感知機(jī)精確表示。這本書的出版給整個(gè)神經(jīng)網(wǎng)絡(luò)領(lǐng)域的發(fā)展帶來了巨大負(fù)面影響。究其原因，明斯基和佩珀特的出發(fā)點(diǎn)是錯(cuò)誤的：我們應(yīng)該把神經(jīng)網(wǎng)絡(luò)看成是逼近函數(shù)的工具，而不只是看它能夠精確表達(dá)什么函數(shù)。而從函數(shù)逼近的角度來說，神經(jīng)網(wǎng)絡(luò)不僅能夠逼近一般函數(shù)(universal approximation theorem)，而且基于神經(jīng)網(wǎng)絡(luò)的逼近和基于其他傳統(tǒng)方法的逼近有著本質(zhì)區(qū)別：傳統(tǒng)逼近方法有維數(shù)災(zāi)難問題，而神經(jīng)網(wǎng)絡(luò)在高維或者多個(gè)變量的情形下仍然很有效。

當(dāng)然，除了維數(shù)災(zāi)難和組合爆炸之外，還有許多其他問題需要考慮。比如，對(duì)文本這類時(shí)間序列數(shù)據(jù)來說，能否處理長(zhǎng)期記憶(long-term memory)是一個(gè)重要問題。有結(jié)果表明，循環(huán)神經(jīng)網(wǎng)絡(luò)(RNN)有記憶災(zāi)難問題：即當(dāng)記憶長(zhǎng)度增加時(shí)，所需要的神經(jīng)元個(gè)數(shù)呈指數(shù)增加。而transformer網(wǎng)絡(luò)沒有這個(gè)問題。事實(shí)上，有理論結(jié)果表明，transformer網(wǎng)絡(luò)的確能夠有效表達(dá)長(zhǎng)程但稀疏的記憶依賴關(guān)系。這正是大語言模型所需要的。

全數(shù)據(jù)

大數(shù)據(jù)方法考慮的是單個(gè)數(shù)據(jù)集，全數(shù)據(jù)方法的思路是把所有數(shù)據(jù)都用起來。比方說，把互聯(lián)網(wǎng)上所有高質(zhì)量文本數(shù)據(jù)都用起來。這里有兩個(gè)關(guān)鍵問題，一是絕大部分?jǐn)?shù)據(jù)都是無標(biāo)注數(shù)據(jù)，如何用好這些無標(biāo)注數(shù)據(jù)？預(yù)訓(xùn)練方法就是為了解決這個(gè)問題而誕生的。二是既然我們把所有數(shù)據(jù)都用了，就得把所有可能的下游問題都解決了。也就是說，我們的目標(biāo)必須是某種形式的通用人工智能系統(tǒng)。這就催生了有監(jiān)督的微調(diào)（SFT）技術(shù)。

目前這個(gè)思路最成功的實(shí)踐出現(xiàn)在文本領(lǐng)域。對(duì)文本來說，有兩個(gè)最典型的預(yù)訓(xùn)練框架。一是谷歌的BERT，它的出發(fā)點(diǎn)是填空；二是OpenAI的GPT，它的技術(shù)路線是預(yù)測(cè)下一個(gè)詞。就目前的發(fā)展情況來看，GPT占了絕對(duì)優(yōu)勢(shì)。究其原因，是BERT試圖靠上下文內(nèi)容進(jìn)行語義理解（雙向預(yù)測(cè)），而GPT只根據(jù)過去預(yù)測(cè)未來（單向預(yù)測(cè)），所以GPT既是一個(gè)生成模型，又是文本任務(wù)的一個(gè)通用模型：只要能夠預(yù)測(cè)下一個(gè)詞，我們就可以解決文本領(lǐng)域的所有問題，包括翻譯、對(duì)話、寫作等。從智能的角度來說，如果一個(gè)機(jī)器能夠在不同場(chǎng)景下把預(yù)測(cè)下一個(gè)詞的任務(wù)做好，那么它的文本能力就不低于人類。也就是說，它具備了一定的智能的本質(zhì)特性。相比較而言，BERT完成的是一個(gè)更加簡(jiǎn)單的任務(wù)，因?yàn)樗軌蚶煤竺娴奈谋緝?nèi)容幫助完成填空問題，所以它不需要很強(qiáng)的智能能力。

從理論上來看，大模型帶來的最突出的現(xiàn)象是縮放定律(scaling law)和相應(yīng)的涌現(xiàn)現(xiàn)象(emergent behavior)。縮放定律源于復(fù)雜系統(tǒng)研究，是指當(dāng)系統(tǒng)規(guī)模變大時(shí)，相關(guān)指標(biāo)會(huì)按照一定的規(guī)律變化。在大模型領(lǐng)域，它有兩方面的意義。一方面，它讓我們可以從訓(xùn)練小一點(diǎn)的模型出發(fā)，估算出訓(xùn)練大模型所需要的計(jì)算量和數(shù)據(jù)資源；另一方面，它為提升模型的功能提供了一個(gè)指導(dǎo)方向。從后者的角度來看，縮放定律起的作用有點(diǎn)像摩爾定律。

應(yīng)該強(qiáng)調(diào)的是，縮放定律和涌現(xiàn)都是在復(fù)雜系統(tǒng)中經(jīng)常能看到的現(xiàn)象。不同的技術(shù)框架可以有不同的縮放定律，而優(yōu)化縮放定律應(yīng)該是我們追求的主要目標(biāo)之一。當(dāng)然，我們也可以問：就像摩爾定律一樣，縮放定律終究會(huì)有停滯的時(shí)候，下一步該如何發(fā)展？

我們還可以把這些不同方法組合在一起，構(gòu)建更加有效的方法。一個(gè)例子是DeepMind推出的AlphaGeometry，它求解國際奧林匹克數(shù)學(xué)競(jìng)賽中平面幾何題目的能力接近了人類最高水平（見圖2）。它的主要想法是把邏輯推理方法和經(jīng)驗(yàn)方法相結(jié)合：定理庫和樹搜索提供具體證明，而機(jī)器學(xué)習(xí)模型提供思路，比如如何加輔助線。毫無疑問，這類想法有著巨大的發(fā)展空間。

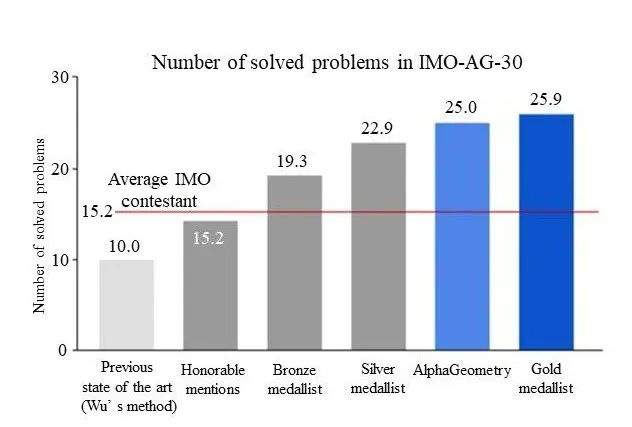
圖2 AlphaGeometry將目前模型的幾何定理證明水平從低于人類水平提高到接近金牌水平

從長(zhǎng)遠(yuǎn)的角度來看，目前以GPT為代表的技術(shù)路徑并不適合我國的國情。首先，在相當(dāng)長(zhǎng)的一段時(shí)間里，我國的算力與美國的相比將會(huì)有相當(dāng)大的差距。目前國內(nèi)大模型第一梯隊(duì)的算力資源基本上是萬卡規(guī)模（比如英偉達(dá)A100），而美國第一梯隊(duì)是10萬卡甚至更大規(guī)模。這就意味著在不遠(yuǎn)的未來，許多致力于開發(fā)基座模型的團(tuán)隊(duì)可能不得不停下追趕的腳步。其次，GPT存在許多浪費(fèi)。我們應(yīng)該尋找更加低能耗、低成本的替代路徑。最近推出的“憶立方”（Memory3）模型就是一種這樣的嘗試。它用內(nèi)置數(shù)據(jù)庫的辦法處理（顯性）知識(shí)，避免把知識(shí)都存放到模型參數(shù)中，這樣可以大大降低對(duì)模型規(guī)模的要求。最后，GPT并不能解決所有問題。在許多方面，比如圖像，我們還需要尋求更加有效的技術(shù)方案。

什么才是適合我國國情的人工智能發(fā)展路徑？如何才能保證我國的人工智能長(zhǎng)期穩(wěn)定地發(fā)展？要回答這些問題，我們必須在以下兩方面盡快布局。一是建立起一個(gè)完整的人工智能底層創(chuàng)新團(tuán)隊(duì)和創(chuàng)新體系，在模型架構(gòu)、AI系統(tǒng)、數(shù)據(jù)處理工具、高效訓(xùn)練芯片等方向追求新突破；二是探索人工智能的基本原理，盡管我們與掌握人工智能的基本原理還有很大差距，但是我們已經(jīng)具備了探索這些基本原理的條件。而長(zhǎng)期穩(wěn)定發(fā)展的技術(shù)路線，必然會(huì)在這個(gè)探索過程中產(chǎn)生出來。

致謝：在這篇文章的寫作和院士大會(huì)報(bào)告的準(zhǔn)備過程中，我得到了黃鐵軍、楊泓康、袁坤、朱松純等老師的幫助。在此一并表示感謝！

鄂維南

CCF會(huì)士。中國科學(xué)院院士。北京大學(xué)教授。主要研究方向?yàn)闄C(jī)器學(xué)習(xí)、計(jì)算數(shù)學(xué)、應(yīng)用數(shù)學(xué)及其在化學(xué)、材料科學(xué)和流體力學(xué)中的應(yīng)用。weinan@math.pku.edu.cn

聲明：本文來自中國計(jì)算機(jī)學(xué)會(huì)，稿件和圖片版權(quán)均歸原作者所有。所涉觀點(diǎn)不代表東方安全立場(chǎng)，轉(zhuǎn)載目的在于傳遞更多信息。如有侵權(quán)，請(qǐng)聯(lián)系rhliu@skdlabs.com，我們將及時(shí)按原作者或權(quán)利人的意愿予以更正。